Étiquette : humour

Darie blogue (principe et loi)  nous rappelle deux lois fondamentales : La loi de Pareto dont j’ai parlé quand j’étais confortablement installé dans un placard de luxe et du principe de la Grenouille (Le Paradoxe de la grenouille. Jusqu’à là tout va bien)

En terme de loi empiriques j’aime particulièrement

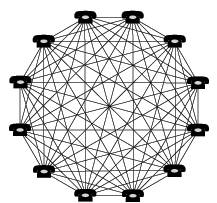
La loi de Metcalfe : « L’utilité d’un réseau est proportionnelle au carré du nombre de ses utilisateurs » loi qui marche pour les réseaux sociaux et la téléphonie. Si il existe un téléphone au monde ça ne sert à rien, deux, ça limite l’usage…

La loi de la Tartine Beurrée : Elle tombe toujours du côté de la confiture (archi connu) qui fait partie de la loi de Murphy

La loi de Moore, qui dit que la puissance des microprocesseurs croit de deux fois tous les 18 mois

Loi de Zipf que j’ai adaptée pour apprendre une langue, méthode statistique qui fait qu’on ne doit apprendre que les mots les plus répétés, ainsi avec une bonne centaine de mots on peut déjà balbutier quelque chose

La loi de Parkinson, que j’aurais du noter il y a bien longtemps « le travail s’étale de façon à occuper le temps disponible pour son achèvement » (source wikipedia) avec « Un fonctionnaire entend multiplier ses subordonnés, pas ses rivaux » et « Les fonctionnaires se créent mutuellement du travail ». Mon expérience dans le privé me fait dire qu’il n’y pas que les fonctionnaires, lire le livre « Bonjour Paresse ».

Cela dit il y a la loi de Hofstadter qui dit « Ça prend toujours plus de temps qu’on croit, même en prenant en compte la loi de Hofstadter » (toujours source wikipedia)

La loi de Stein : I »f something cannot go on forever, it will stop ». Pour les pessimistes, si t’es joyeux ça va pas durer « un malheur n’arrive pas sans l’autre » pour les optimistes « l’heure la plus sombre de la nuit est celle qui précede le début du jour » (c’est chinois)

🙂